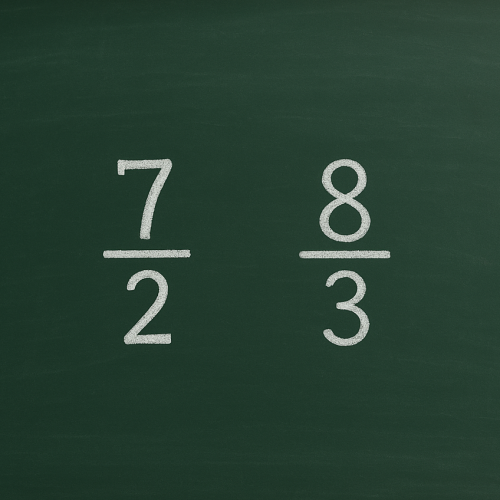
Тест по математике: Выделение целой части дроби (5 класс)

Пояснение:

Для выделения целой части из неправильной дроби необходимо разделить числитель на знаменатель. Целая часть будет равна частному от деления (без остатка), а дробная часть — это остаток от деления, записанный над знаменателем исходной дроби. Например, чтобы выделить целую часть из дроби 17/5, нужно разделить 17 на 5: 17 ÷ 5 = 3 (частное) и остаток 2. Значит, 17/5 = 3⅖. Этот метод позволяет преобразовать любую неправильную дробь (числитель больше знаменателя) в смешанное число, что часто более наглядно для понимания величины дроби.

Пояснение:

Чтобы выделить целую часть из дроби 11/4, нужно разделить числитель (11) на знаменатель (4): 11 ÷ 4 = 2 (частное) и остаток 3. Целая часть смешанного числа будет равна 2, а дробная часть — это остаток от деления (3) над знаменателем исходной дроби (4), то есть 3/4. Таким образом, дробь 11/4 в виде смешанного числа записывается как 2 3/4.

Это преобразование можно проверить, выполнив обратное действие: 2 3/4 = 2 + 3/4 = (2 × 4 + 3)/4 = (8 + 3)/4 = 11/4.

Пояснение:

Чтобы выделить целую часть из дроби 23/6, нужно разделить числитель (23) на знаменатель (6): 23 ÷ 6 = 3 (частное) и остаток 5. Целая часть смешанного числа будет равна 3, а дробная часть — это остаток от деления (5) над знаменателем исходной дроби (6), то есть 5/6. Таким образом, дробь 23/6 в виде смешанного числа записывается как 3 5/6.

Можно проверить: 3 5/6 = 3 + 5/6 = (3 × 6 + 5)/6 = (18 + 5)/6 = 23/6, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 7/2, нужно разделить числитель (7) на знаменатель (2): 7 ÷ 2 = 3 (частное) и остаток 1. Целая часть смешанного числа будет равна 3, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (2), то есть 1/2. Таким образом, дробь 7/2 в виде смешанного числа записывается как 3 1/2.

Проверка: 3 1/2 = 3 + 1/2 = (3 × 2 + 1)/2 = (6 + 1)/2 = 7/2, что совпадает с исходной дробью, подтверждая правильность нашего преобразования.

Пояснение:

Чтобы выделить целую часть из дроби 19/5, нужно разделить числитель (19) на знаменатель (5): 19 ÷ 5 = 3 (частное) и остаток 4. Целая часть смешанного числа будет равна 3, а дробная часть — это остаток от деления (4) над знаменателем исходной дроби (5), то есть 4/5. Таким образом, дробь 19/5 в виде смешанного числа записывается как 3 4/5.

Проверим: 3 4/5 = 3 + 4/5 = (3 × 5 + 4)/5 = (15 + 4)/5 = 19/5, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 29/8, нужно разделить числитель (29) на знаменатель (8): 29 ÷ 8 = 3 (частное) и остаток 5. Целая часть смешанного числа будет равна 3, а дробная часть — это остаток от деления (5) над знаменателем исходной дроби (8), то есть 5/8. Таким образом, дробь 29/8 в виде смешанного числа записывается как 3 5/8.

Проверим правильность: 3 5/8= 3 + 5/8 = (3 × 8 + 5)/8 = (24 + 5)/8 = 29/8, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 13/3, нужно разделить числитель (13) на знаменатель (3): 13 ÷ 3 = 4 (частное) и остаток 1. Целая часть смешанного числа будет равна 4, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (3), то есть 1/3. Таким образом, дробь 13/3 в виде смешанного числа записывается как 4 1/3.

Можно проверить: 4 1/3 = 4 + 1/3 = (4 × 3 + 1)/3 = (12 + 1)/3 = 13/3, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 27/4, нужно разделить числитель (27) на знаменатель (4): 27 ÷ 4 = 6 (частное) и остаток 3. Целая часть смешанного числа будет равна 6, а дробная часть — это остаток от деления (3) над знаменателем исходной дроби (4), то есть 3/4. Таким образом, дробь 27/4 в виде смешанного числа записывается как 6 3/4.

Проверим:

6 3/4 = 6 + 3/4 = (6 × 4 + 3)/4 = (24 + 3)/4 = 27/4, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 43/7, нужно разделить числитель (43) на знаменатель (7): 43 ÷ 7 = 6 (частное) и остаток 1. Целая часть смешанного числа будет равна 6, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (7), то есть 1/7. Таким образом, дробь 43/7 в виде смешанного числа записывается как 6 1/7.

Проверим: 6 1/7 = 6 + 1/7 = (6 × 7 + 1)/7 = (42 + 1)/7 = 43/7, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 31/9, нужно разделить числитель (31) на знаменатель (9): 31 ÷ 9 = 3 (частное) и остаток 4. Целая часть смешанного числа будет равна 3, а дробная часть — это остаток от деления (4) над знаменателем исходной дроби (9), то есть 2/3. Таким образом, дробь 31/9 в виде смешанного числа записывается как 3 2/3. Запись 3 2/3 означает 3 и 2/3, или 3 + 2/3.

Проверим:

3 2/3 = 3 + 2/3 = (3 × 9 + 4)/9 = (27 + 4)/9 = 31/9, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 37/6, нужно разделить числитель (37) на знаменатель (6): 37 ÷ 6 = 6 (частное) и остаток 1. Целая часть смешанного числа будет равна 6, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (6), то есть 1/6. Таким образом, дробь 37/6 в виде смешанного числа записывается как 6 1/6. Проверим: 6 1/6 = 6 + 1/6= (6 × 6 + 1)/6 = (36 + 1)/6 = 37/6, что соответствует исходной дроби.

Пояснение:

Выделение целой части из неправильной дроби означает преобразование неправильной дроби (у которой числитель больше или равен знаменателю) в смешанное число, состоящее из целой и дробной части. Этот процесс включает деление числителя на знаменатель, где частное становится целой частью, а остаток от деления — числителем дробной части при том же знаменателе. Например, выделяя целую часть из дроби 17/5, получаем смешанное число 3⅖. Такое преобразование делает значение дроби более наглядным и понятным, особенно при решении практических задач.

Пояснение:

Чтобы выделить целую часть из дроби 47/8, нужно разделить числитель (47) на знаменатель (8): 47 ÷ 8 = 5 (частное) и остаток 7. Целая часть смешанного числа будет равна 5, а дробная часть — это остаток от деления (7) над знаменателем исходной дроби (8), то есть 7/8. Таким образом, дробь 47/8 в виде смешанного числа записывается как 5 7/8.

Проверим:

5 7/8 = 5 + 7/8 = (5 × 8 + 7)/8 = (40 + 7)/8 = 47/8, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 53/10, нужно разделить числитель (53) на знаменатель (10): 53 ÷ 10 = 5 (частное) и остаток 3. Целая часть смешанного числа будет равна 5, а дробная часть — это остаток от деления (3) над знаменателем исходной дроби (10), то есть 3/5. Таким образом, дробь 53/10 в виде смешанного числа записывается как 5 3/5.

Проверим:

5 3/5 = 5 + 3/5 = (5 × 10 + 3)/10 = (50 + 3)/10 = 53/10, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 25/3, нужно разделить числитель (25) на знаменатель (3): 25 ÷ 3 = 8 (частное) и остаток 1. Целая часть смешанного числа будет равна 8, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (3), то есть 1/3. Таким образом, дробь 25/3 в виде смешанного числа записывается как 8 1/3.

Проверим: 8 1/3 = 8 + 1/3 = (8 × 3 + 1)/3 = (24 + 1)/3 = 25/3, что совпадает с исходной дробью.

Пояснение:

Чтобы выделить целую часть из дроби 61/12, нужно разделить числитель (61) на знаменатель (12): 61 ÷ 12 = 5 (частное) и остаток 1. Целая часть смешанного числа будет равна 5, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (12), то есть 1/12. Таким образом, дробь 61/12 в виде смешанного числа записывается как 5 1/12.

Проверим: 5 1/12 = 5 + 1/12 = (5 × 12 + 1)/12 = (60 + 1)/12 = 61/12, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 17/4, нужно разделить числитель (17) на знаменатель (4): 17 ÷ 4 = 4 (частное) и остаток 1. Целая часть смешанного числа будет равна 4, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (4), то есть 1/4. Таким образом, дробь 17/4 в виде смешанного числа записывается как 4 1/4.

Проверим: 4 1/4 = 4 + 1/4 = (4 × 4 + 1)/4 = (16 + 1)/4 = 17/4, что совпадает с исходной дробью.

Пояснение:

Чтобы из дроби можно было выделить целую часть, она должна быть неправильной, то есть такой, у которой числитель больше или равен знаменателю. Только в этом случае при делении числителя на знаменатель получится ненулевое частное, которое станет целой частью смешанного числа. Например, из дроби 7/3 можно выделить целую часть, так как 7 > 3, и получить смешанное число 2 1/3. Из правильной дроби, например 2/5, нельзя выделить целую часть, так как при делении 2 на 5 получится 0 в частном и 2 в остатке, то есть дробь останется без изменений.

Пояснение:

Чтобы выделить целую часть из дроби 41/5, нужно разделить числитель (41) на знаменатель (5): 41 ÷ 5 = 8 (частное) и остаток 1. Целая часть смешанного числа будет равна 8, а дробная часть — это остаток от деления (1) над знаменателем исходной дроби (5), то есть 1/5. Таким образом, дробь 41/5 в виде смешанного числа записывается как 8 1/5.

Проверим: 8 1/5 = 8 + 1/5 = (8 × 5 + 1)/5 = (40 + 1)/5 = 41/5, что соответствует исходной дроби.

Пояснение:

Чтобы выделить целую часть из дроби 59/9, нужно разделить числитель (59) на знаменатель (9): 59 ÷ 9 = 6 (частное) и остаток 5. Целая часть смешанного числа будет равна 6, а дробная часть — это остаток от деления (5) над знаменателем исходной дроби (9), то есть 5/9. Таким образом, дробь 59/9 в виде смешанного числа записывается как 6 5/9. Проверим: 6 5/9 = 6 + 1/9 = (6 × 9 + 5)/9 = (54 + 5)/9 = 59/9, что соответствует исходной дроби.