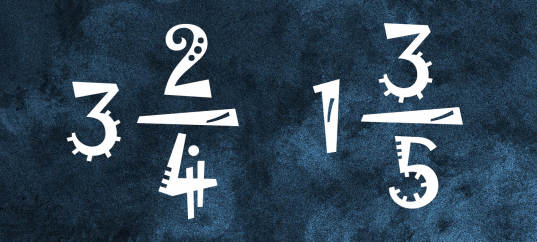Самостоятельная работа: Сложение дробей
Самостоятельная работа по теме «Сложение дробей» — это интерактивное проверочное задание, рассчитанное на учащихся 5-6 класса. Проверьте свои знания и навыки по сложению обыкновенных дробей с одинаковыми и разными знаменателями, а также смешанных чисел.
Правильный ответ:
5/7Пояснение:
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним. В данном примере 2/7 + 3/7 = (2+3)/7 = 5/7. Правило сложения дробей с одинаковыми знаменателями можно записать формулой: a/c + b/c = (a+b)/c. Это одно из базовых правил работы с дробями, которое используется при решении многих задач. Важно помнить, что знаменатель не меняется, когда мы складываем дроби с одинаковыми знаменателями.
Правильный ответ:
1Пояснение:
При сложении дробей с одинаковыми знаменателями мы складываем числители и сохраняем тот же знаменатель: 1/4 + 3/4 = (1+3)/4 = 4/4 = 1. Дробь 4/4 означает 4 части из 4, то есть целую единицу, поэтому 4/4 = 1. Важно уметь сокращать дроби и переводить их в целые числа, когда числитель и знаменатель равны. Это помогает представить результат в наиболее простом виде, что является обязательным требованием при работе с дробями.
Правильный ответ:
1/2Пояснение:
При сложении дробей с одинаковыми знаменателями: 3/8 + 1/8 = (3+1)/8 = 4/8. Дробь 4/8 можно сократить, разделив и числитель, и знаменатель на их общий делитель 4. Получаем 4/8 = (4÷4)/(8÷4) = 1/2. В математике всегда требуется представлять результат в наиболее простом виде, поэтому важно уметь сокращать дроби. Дробь считается несократимой, если числитель и знаменатель не имеют общих делителей, кроме 1.
Правильный ответ:
2/3Пояснение:
При сложении дробей с одинаковыми знаменателями: 5/12 + 3/12 = (5+3)/12 = 8/12. Дробь 8/12 можно сократить, разделив и числитель, и знаменатель на их наибольший общий делитель 4. Тогда 8/12 = (8÷4)/(12÷4) = 2/3. Умение сокращать дроби — важный навык в работе с дробями. Для этого нужно найти наибольший общий делитель числителя и знаменателя, а затем разделить на него обе части дроби. В данном случае НОД(8, 12) = 4.
Правильный ответ:
5/6Пояснение:
При сложении дробей с разными знаменателями нужно привести их к общему знаменателю. Наименьший общий знаменатель для 3 и 6 равен 6. 2/3 = 2·2/3·2 = 4/6. Теперь можно сложить: 4/6 + 1/6 = (4+1)/6 = 5/6. Приведение дробей к общему знаменателю — это умножение числителя и знаменателя одной дроби на такое число, чтобы знаменатели обеих дробей стали одинаковыми. При этом значение дроби не меняется, так как мы умножаем её на 1 в виде дроби (например, 2/2 = 1).
Правильный ответ:
5/6Пояснение:
Для сложения дробей с разными знаменателями находим наименьший общий знаменатель (НОК) для 2 и 3, это 6. Приводим дроби к новому знаменателю: 1/2 = 1·3/2·3 = 3/6, 1/3 = 1·2/3·2 = 2/6. Теперь складываем: 3/6 + 2/6 = (3+2)/6 = 5/6. Умение находить наименьшее общее кратное (НОК) и приводить дроби к общему знаменателю — важный навык при работе с дробями. НОК чисел — это наименьшее натуральное число, которое делится на эти числа без остатка.
Правильный ответ:
17/12Пояснение:
Для сложения дробей с разными знаменателями найдем НОК(4, 3) = 12. Приведем дроби к знаменателю 12: 3/4 = 3·3/4·3 = 9/12, 2/3 = 2·4/3·4 = 8/12. Складываем дроби с одинаковыми знаменателями: 9/12 + 8/12 = (9+8)/12 = 17/12. Результат можно записать и как смешанное число: 17/12 = 1 5/12, но в данном примере требуется оставить ответ в виде неправильной дроби. Умение работать и с неправильными дробями, и со смешанными числами важно в математике.
Правильный ответ:
17/18Пояснение:
Для сложения дробей с разными знаменателями находим НОК(9, 6) = 18. Приводим дроби к общему знаменателю: 2/9 = 2·2/9·2 = 4/18, 5/6 = 5·3/6·3 = 15/18. Складываем: 4/18 + 15/18 = (4+15)/18 = 19/18. Дробь можно сократить: 19/18 = 17/18. При нахождении НОК полезно разложить числа на простые множители: 9 = 3², 6 = 2·3, поэтому НОК(9, 6) = 2·3² = 18. Это помогает точно определить наименьший общий знаменатель, к которому нужно привести дроби.
Правильный ответ:
7/8Пояснение:
Для сложения дробей с разными знаменателями находим НОК(8, 4) = 8 (так как 8 уже делится на 4). Приводим вторую дробь к знаменателю 8: 3/4 = 3·2/4·2 = 6/8. Теперь складываем: 5/8 + 6/8 = (5+6)/8 = 11/8 = 1 3/8. Дробь 11/8 можно записать как смешанное число 1 3/8, но мы её можно также оставить в виде неправильной дроби. При сложении дробей важно уметь переходить между разными представлениями числа: неправильными дробями и смешанными числами.
Правильный ответ:
3 7/10Пояснение:
Для сложения смешанных чисел сначала отдельно складываем их целые и дробные части. Целые части: 1 + 2 = 3. Для сложения дробных частей находим НОК(5, 10) = 10. Приводим первую дробь к знаменателю 10: 3/5 = 3·2/5·2 = 6/10. Теперь складываем дробные части: 6/10 + 1/10 = 7/10. Итоговый результат: 3 + 7/10 = 3 7/10. При сложении смешанных чисел важно не забывать, что если сумма дробных частей превышает 1, то нужно выделить целую часть и добавить её к сумме целых частей.
Правильный ответ:
5 11/12Пояснение:
При сложении смешанных чисел отдельно складываем целые и дробные части. Целые части: 2 + 3 = 5. Для сложения дробных частей 1/4 и 2/3 находим НОК(4, 3) = 12. Приводим дроби к общему знаменателю: 1/4 = 3/12, 2/3 = 8/12. Складываем дробные части: 3/12 + 8/12 = 11/12. Итоговый результат: 5 + 11/12 = 5 11/12. Такой метод сложения смешанных чисел эффективен, когда сумма дробных частей меньше 1. Если бы сумма дробных частей превысила 1, пришлось бы выделить целую часть.
Правильный ответ:
4 1/10Пояснение:
Складываем целые части: 1 + 2 = 3. Для сложения дробных частей 2/5 и 7/10 находим НОК(5, 10) = 10. Приводим первую дробь к знаменателю 10: 2/5 = 4/10. Складываем дробные части: 4/10 + 7/10 = 11/10 = 1 1/10. Поскольку сумма дробных частей больше 1, добавляем эту единицу к сумме целых частей: 3 + 1 = 4. Итоговый результат: 4 + 1/10 = 4 1/10. Важно помнить, что при сложении смешанных чисел результат нужно представить в виде смешанного числа с правильной дробной частью (меньше 1).
Правильный ответ:
6Пояснение:
Складываем целые части: 3 + 2 = 5. Складываем дробные части с одинаковыми знаменателями: 1/6 + 5/6 = 6/6 = 1. Поскольку дробная часть даёт целую единицу, добавляем её к сумме целых частей: 5 + 1 = 6. Итоговый результат: 6. Обратите внимание, что дробь 6/6 равна 1, поэтому в результате получается целое число. Всегда важно упрощать результат до конца, переводя несократимые дроби вида n/n в целые числа и сокращая дроби при необходимости.
Правильный ответ:
4 3/9Пояснение:
Складываем целые части: 2 + 1 = 3. Складываем дробные части с одинаковыми знаменателями: 7/9 + 5/9 = 12/9 = 1 3/9. Так как дробная часть больше 1, выделяем целую часть (1) и добавляем к сумме целых: 3 + 1 = 4. Итоговый результат: 4 + 3/9 = 4 3/9 или 4 1/3 (после сокращения дроби 3/9 = 1/3). Важный шаг — сокращение дробей в ответе. Дробь 3/9 сокращается на 3, получаем 1/3. Всегда представляйте ответ в самом простом виде.
Правильный ответ:
23/24Пояснение:
Для сложения дробей с разными знаменателями находим НОК(12, 8) = 24. Приводим дроби к общему знаменателю: 5/12 = 5·2/12·2 = 10/24, 3/8 = 3·3/8·3 = 9/24. Складываем: 10/24 + 9/24 = (10+9)/24 = 19/24. Число 19/24 — правильная несократимая дробь, так как числитель меньше знаменателя, а числа 19 и 24 не имеют общих делителей кроме 1. При нахождении НОК полезно разложить числа на простые множители: 12 = 2²·3, 8 = 2³, поэтому НОК(12, 8) = 2³·3 = 24.
Правильный ответ:
16/36Пояснение:
Для сложения дробей с разными знаменателями находим НОК(18, 12) = 36. Приводим дроби к общему знаменателю: 5/18 = 5·2/18·2 = 10/36, 7/12 = 7·3/12·3 = 21/36. Складываем: 10/36 + 21/36 = (10+21)/36 = 31/36. Дробь 31/36 — правильная несократимая дробь. Можно проверить, что 31 и 36 не имеют общих делителей кроме 1, поэтому дробь нельзя сократить. При вычислениях с дробями важно доводить результат до наиболее простого вида, сокращая дробь, если это возможно, или представляя неправильную дробь в виде смешанного числа.
Правильный ответ:
5 1/10Пояснение:
Складываем целые части: 3 + 1 = 4. Для сложения дробных частей 2/5 и 7/10 находим НОК(5, 10) = 10. Приводим первую дробь к знаменателю 10: 2/5 = 2·2/5·2 = 4/10. Складываем дробные части: 4/10 + 7/10 = 11/10 = 1 1/10. Поскольку сумма дробных частей больше 1, добавляем эту единицу к сумме целых: 4 + 1 = 5. Итоговый результат: 5 + 1/10 = 5 1/10. Важно помнить, что при сложении смешанных чисел может потребоваться выделение целой части из суммы дробных частей.
Правильный ответ:
5 19/45Пояснение:
Складываем целые части: 2 + 3 = 5. Для сложения дробных частей 4/15 и 2/9 находим НОК(15, 9) = 45. Приводим дроби к общему знаменателю: 4/15 = 4·3/15·3 = 12/45, 2/9 = 2·5/9·5 = 10/45. Складываем дробные части: 12/45 + 10/45 = 22/45. Для проверки убедимся, что дробь несократима — числа 22 и 45 имеют общий делитель 1, значит, дробь сократить нельзя. Итоговый результат: 5 + 22/45 = 5 22/45.
Правильный ответ:
1Пояснение:
Для сложения трех дробей с разными знаменателями находим НОК(3, 5, 15) = 15. Приводим дроби к общему знаменателю: 1/3 = 1·5/3·5 = 5/15, 2/5 = 2·3/5·3 = 6/15, 1/15 (уже с нужным знаменателем). Складываем: 5/15 + 6/15 + 1/15 = (5+6+1)/15 = 12/15 = 4/5. Дробь 4/5 можно упростить, разделив числитель и знаменатель на их наибольший общий делитель 4. Получаем 4/5 = (4÷4)/(5÷4) = 1. При работе с несколькими дробями полезно привести их все к общему знаменателю сразу, а затем выполнить сложение.
Правильный ответ:
3 1/2Пояснение:
Сначала складываем целые части: 1 + 2 = 3. Для сложения дробных частей 1/6, 1/4 и 3/12 находим НОК(6, 4, 12) = 12. Приводим дроби к общему знаменателю: 1/6 = 2/12, 1/4 = 3/12, 3/12 (уже с нужным знаменателем). Складываем дробные части: 2/12 + 3/12 + 3/12 = 8/12 = 2/3. Дробь 2/3 сократить нельзя, так как 2 и 3 не имеют общих делителей кроме 1. Но можно представить 2/3 как 4/6, а затем как 6/12, что даёт 1/2. Итоговый результат: 3 + 1/2 = 3 1/2.