Тест по математике: Координаты (6 класс)
Тест по математике «Координаты» — это интерактивная проверочная (контрольная) работа онлайн, рассчитанная на учащихся 6 класса. Проверяет знания о координатной плоскости, координатах точек, умение строить точки по заданным координатам и определять координаты точек на плоскости.
Правильный ответ:
Плоскость с двумя взаимно перпендикулярными осями координат.Пояснение:
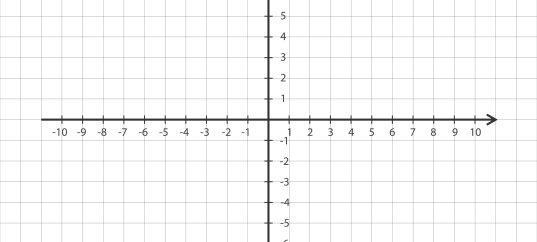
Координатная плоскость — это плоскость с двумя взаимно перпендикулярными числовыми осями (осью абсцисс и осью ординат), которые пересекаются в начале координат. Эти две оси задают систему координат на плоскости, позволяя однозначно определить положение любой точки с помощью пары чисел — координат этой точки. Благодаря координатной плоскости мы можем графически представлять зависимости между величинами, решать уравнения и строить геометрические фигуры.
Правильный ответ:
Ось абсцисс (ось X)Пояснение:
Горизонтальная ось координатной плоскости называется осью абсцисс или осью X. По этой оси откладываются значения первой координаты точки (абсциссы). Ось абсцисс направлена слева направо, при этом положительные значения откладываются вправо от начала координат, а отрицательные — влево. Ось абсцисс вместе с осью ординат образуют прямоугольную (декартову) систему координат на плоскости.
Правильный ответ:
Ось ординат (ось Y)Пояснение:
Вертикальная ось координатной плоскости называется осью ординат или осью Y. По этой оси откладываются значения второй координаты точки (ординаты). Ось ординат направлена снизу вверх, при этом положительные значения откладываются вверх от начала координат, а отрицательные — вниз. Ось ординат вместе с осью абсцисс образуют прямоугольную (декартову) систему координат на плоскости.
Правильный ответ:
Началом координатПояснение:
Точка пересечения осей координат на координатной плоскости называется началом координат. Эта точка имеет координаты (0; 0). От начала координат ведется отсчет по обеим осям: по оси абсцисс (X) — вправо и влево, по оси ординат (Y) — вверх и вниз. Начало координат является точкой отсчета в прямоугольной (декартовой) системе координат и играет важную роль при определении положения других точек на плоскости.
Правильный ответ:
(0; 0)Пояснение:
Начало координат — это точка пересечения осей координат, которая имеет координаты (0; 0). Это означает, что и абсцисса (первая координата), и ордината (вторая координата) этой точки равны нулю. Начало координат является точкой отсчета для обеих осей координатной плоскости. От этой точки вправо по оси абсцисс и вверх по оси ординат откладываются положительные значения соответствующих координат, а влево и вниз — отрицательные значения.Правильный ответ:
(−3; 4)Пояснение:
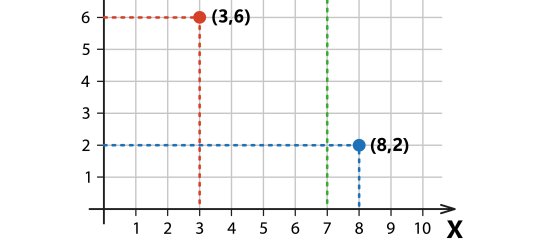
Чтобы определить координаты точки на координатной плоскости, нужно найти значение абсциссы (первой координаты) и ординаты (второй координаты). Абсцисса — это расстояние от оси ординат до точки, со знаком «+», если точка справа от оси ординат, и со знаком «−», если точка слева. Ордината — это расстояние от оси абсцисс до точки, со знаком «+», если точка выше оси абсцисс, и со знаком «−», если точка ниже. В данном случае точка имеет координаты (−3; 4).
Правильный ответ:
IV четвертьПояснение:
Координатная плоскость разделена на четыре четверти: I четверть — где обе координаты положительны (x > 0, y > 0); II четверть — где x < 0, y > 0; III четверть — где обе координаты отрицательны (x < 0, y < 0); IV четверть — где x > 0, y < 0. Точка с координатами (−5; −3) имеет отрицательную абсциссу (x = −5) и отрицательную ординату (y = −3), следовательно, она находится в III четверти координатной плоскости, а не в IV, как было указано ошибочно.Правильный ответ:
IV четвертьПояснение:
Координатная плоскость разделена осями на четыре четверти. В I четверти обе координаты положительны (x > 0, y > 0), во II четверти x < 0, y > 0, в III четверти обе координаты отрицательны (x < 0, y < 0), а в IV четверти x > 0, y < 0. Точка с координатами (4; −2) имеет положительную абсциссу (x = 4) и отрицательную ординату (y = −2), поэтому она находится в IV четверти координатной плоскости.Правильный ответ:
II четвертьПояснение:
Координатная плоскость делится осями координат на четыре четверти. В I четверти обе координаты положительны (x > 0, y > 0), во II четверти абсцисса отрицательна, а ордината положительна (x < 0, y > 0), в III четверти обе координаты отрицательны (x < 0, y < 0), в IV четверти абсцисса положительна, а ордината отрицательна (x > 0, y < 0). Точка с координатами (−3; 5) имеет отрицательную абсциссу (x = −3) и положительную ординату (y = 5), следовательно, она находится во II четверти.Правильный ответ:
I четвертьПояснение:
Координатная плоскость разделена на четыре четверти осями координат. Точки, у которых обе координаты положительны (x > 0, y > 0), находятся в I четверти. Точки, у которых x < 0, y > 0, находятся во II четверти. Точки, у которых обе координаты отрицательны (x < 0, y < 0), находятся в III четверти. Точки, у которых x > 0, y < 0, находятся в IV четверти. Точка с координатами (2; 7) имеет положительную абсциссу (x = 2) и положительную ординату (y = 7), поэтому она находится в I четверти.
Правильный ответ:
На оси ординат (оси Y).Пояснение:
Точка с координатами (0; −4) имеет нулевую абсциссу (x = 0) и отрицательную ординату (y = −4). Все точки, у которых абсцисса равна нулю (x = 0), лежат на оси ординат (оси Y), а все точки, у которых ордината равна нулю (y = 0), лежат на оси абсцисс (оси X). Поскольку у данной точки x = 0, она лежит на оси ординат. Конкретно, она расположена на 4 единицы ниже начала координат, так как ордината отрицательна (y = −4).
Правильный ответ:
На оси абсцисс (оси X).Пояснение:
Точка с координатами (5; 0) имеет положительную абсциссу (x = 5) и нулевую ординату (y = 0). Точки, у которых ордината равна нулю (y = 0), лежат на оси абсцисс (оси X). Точки, у которых абсцисса равна нулю (x = 0), лежат на оси ординат (оси Y). Поскольку у данной точки y = 0, она лежит на оси абсцисс. Конкретно, она расположена на 5 единиц правее начала координат, так как абсцисса положительна (x = 5).
Правильный ответ:
C(0; 4)Пояснение:
На оси абсцисс (оси X) лежат точки, у которых ордината равна нулю (y = 0). Точки A(5; 0) и B(−3; 0) имеют нулевую ординату, поэтому они лежат на оси абсцисс. Точка D(0; 0) — это начало координат, она лежит на пересечении оси абсцисс и оси ординат, поэтому также принадлежит оси абсцисс. Точка C(0; 4) имеет нулевую абсциссу и ненулевую ординату, следовательно, она лежит на оси ординат и не принадлежит оси абсцисс.Правильный ответ:
(3; 4)Пояснение:
При симметрии относительно оси абсцисс (оси X) абсцисса точки не меняется, а ордината меняет знак на противоположный. То есть, если координаты точки A(x; y), то координаты точки A«, симметричной ей относительно оси абсцисс, будут A»(x; −y). В данном случае для точки A(3; −4) симметричная ей точка относительно оси абсцисс будет иметь координаты (3; 4), так как абсцисса осталась прежней (x = 3), а ордината изменила знак с отрицательного на положительный (y = −(−4) = 4).Правильный ответ:
(2; 5)Пояснение:
При симметрии относительно оси ординат (оси Y) абсцисса точки меняет знак на противоположный, а ордината остается без изменений. То есть, если координаты точки B(x; y), то координаты точки B«, симметричной ей относительно оси ординат, будут B»(−x; y). В данном случае для точки B(−2; 5) симметричная ей точка относительно оси ординат будет иметь координаты (2; 5), так как абсцисса изменила знак с отрицательного на положительный (x = −(−2) = 2), а ордината осталась прежней (y = 5).Правильный ответ:
(−4; −6)Пояснение:
При симметрии относительно начала координат обе координаты точки меняют знак на противоположный. То есть, если координаты точки C(x; y), то координаты точки C«, симметричной ей относительно начала координат, будут C»(−x; −y). В данном случае для точки C(4; 6) симметричная ей точка относительно начала координат будет иметь координаты (−4; −6), так как абсцисса изменила знак с положительного на отрицательный (x = −4), и ордината также изменила знак с положительного на отрицательный (y = −6).Правильный ответ:
6Пояснение:
Расстояние между точками A(x₁; y₁) и B(x₂; y₂) вычисляется по формуле: d = √((x₂ - x₁)² + (y₂ - y₁)²). В данном случае для точек A(−2; 3) и B(4; 3) имеем: d = √((4 - (−2))² + (3 - 3)²) = √(6² + 0²) = √36 = 6. Обратите внимание, что в данной задаче обе точки имеют одинаковую ординату (y = 3), то есть лежат на одной горизонтальной прямой, поэтому расстояние между ними равно модулю разности их абсцисс: d = |x₂ - x₁| = |4 - (−2)| = |6| = 6.
Правильный ответ:
5Пояснение:
Расстояние между точками C(x₁; y₁) и D(x₂; y₂) вычисляется по формуле: d = √((x₂ - x₁)² + (y₂ - y₁)²). В данном случае для точек C(1; −3) и D(1; 2) имеем: d = √((1 - 1)² + (2 - (−3))²) = √(0² + 5²) = √25 = 5. Обратите внимание, что в данной задаче обе точки имеют одинаковую абсциссу (x = 1), то есть лежат на одной вертикальной прямой, поэтому расстояние между ними равно модулю разности их ординат: d = |y₂ - y₁| = |2 - (−3)| = |5| = 5.Правильный ответ:
разностороннего треугольникаПояснение:
Чтобы определить тип треугольника, нужно найти длины всех его сторон. Расстояние между точками вычисляется по формуле: d = √((x₂ - x₁)² + (y₂ - y₁)²). Найдем длины сторон треугольника ABC: AB = √((3 - (-1))² + (4 - 2)²) = √(4² + 2²) = √(16 + 4) = √20 ≈ 4,47; BC = √((5 - 3)² + (0 - 4)²) = √(2² + (-4)²) = √(4 + 16) = √20 ≈ 4,47; AC = √((5 - (-1))² + (0 - 2)²) = √(6² + (-2)²) = √(36 + 4) = √40 ≈ 6,32. Поскольку все стороны имеют разную длину (хотя AB и BC приблизительно равны, их точное значение — √20), этот треугольник является разносторонним.
Правильный ответ:
КвадратПояснение:
Чтобы определить, какую фигуру образуют точки A(−2; 2), B(2; 2), C(2; −2) и D(−2; −2), найдем длины всех сторон этого четырехугольника. AB = √((2 - (-2))² + (2 - 2)²) = √(4² + 0²) = 4; BC = √((2 - 2)² + (-2 - 2)²) = √(0² + (-4)²) = 4; CD = √((-2 - 2)² + (-2 - (-2))²) = √((-4)² + 0²) = 4; DA = √((-2 - (-2))² + (2 - (-2))²) = √(0² + 4²) = 4. Все стороны равны, что характерно для ромба и квадрата. Проверим диагонали: AC = √((2 - (-2))² + (-2 - 2)²) = √(4² + (-4)²) = √(16 + 16) = √32 ≈ 5,66; BD = √((2 - (-2))² + (-2 - 2)²) = √(4² + (-4)²) = √(16 + 16) = √32 ≈ 5,66. Диагонали равны, следовательно, это квадрат.