Тест по математике: Параллельность прямых (6 класс)

Пояснение:

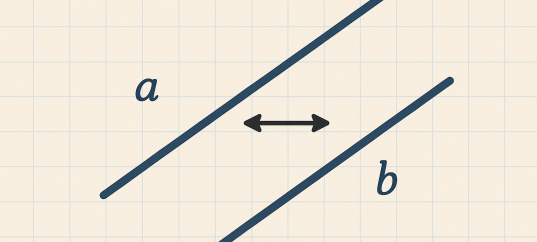
Параллельными называются прямые, которые лежат в одной плоскости и не пересекаются. Это фундаментальное определение в геометрии. Даже если продолжить эти прямые бесконечно в обоих направлениях, они никогда не пересекутся. Расстояние между такими прямыми всегда остается постоянным. В отличие от пересекающихся прямых, которые имеют общую точку, или скрещивающихся прямых, которые лежат в разных плоскостях, параллельные прямые всегда находятся на одинаковом расстоянии друг от друга.

Пояснение:

Между параллельными прямыми нет угла, потому что угол - это фигура, образованная двумя лучами, исходящими из одной точки, или двумя прямыми, пересекающимися в одной точке. Поскольку параллельные прямые по определению не пересекаются, то и угла между ними не существует. Это важное геометрическое понятие, которое следует помнить при решении задач на параллельность. Если говорить о направлениях прямых, то они совпадают, но сами прямые не имеют общей точки, поэтому угол не определен.

Пояснение:

Это утверждение является одной из аксиом евклидовой геометрии (аксиомой параллельности). Согласно этой аксиоме, через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Данная аксиома сформулирована Евклидом и является фундаментальной для построения всей евклидовой геометрии. Она позволяет однозначно определить взаимное расположение прямых в пространстве и является основой для доказательства многих теорем о параллельных прямых.

Пояснение:

Параллельность прямых a и b обозначается символом «∥» и записывается как a ∥ b. Этот математический символ используется во всем мире для обозначения отношения параллельности между геометрическими объектами. Символ похож на две вертикальные линии и визуально отражает суть параллельности - две прямые, которые никогда не пересекаются. Важно не путать этот символ с другими математическими обозначениями, например, с = (равенство), × (умножение) или ⊥ (перпендикулярность).

Пояснение:

Если две прямые параллельны третьей прямой, то они параллельны между собой. Это свойство называется транзитивностью параллельности. Математически это можно записать так: если a ∥ c и b ∥ c, то a ∥ b. Это свойство широко используется при решении геометрических задач и доказательстве теорем. Транзитивность параллельности является следствием определения параллельности и основных аксиом геометрии, в частности, аксиомы о существовании и единственности прямой, проходящей через данную точку параллельно данной прямой.

Пояснение:

Один из признаков параллельности прямых состоит в том, что при пересечении двух прямых третьей (секущей) соответственные углы равны. Соответственные углы - это углы, расположенные по одну сторону от секущей и по одну сторону от каждой из параллельных прямых. Если эти углы равны, то прямые параллельны. Существуют и другие признаки параллельности: равенство накрест лежащих углов или сумма односторонних углов, равная 180°. Эти признаки используются для доказательства параллельности прямых в различных геометрических задачах.

Пояснение:

Прямоугольник, параллелограмм и трапеция содержат параллельные прямые. В прямоугольнике и параллелограмме противоположные стороны параллельны. В трапеции по определению две стороны параллельны (основания), а две другие не параллельны. Эти геометрические фигуры часто изучаются именно в контексте параллельности, так как их свойства напрямую связаны с этим понятием. Понимание параллельности сторон в этих фигурах необходимо для вычисления их площадей, периметров и других характеристик, а также для решения более сложных геометрических задач.

Пояснение:

Параллелограмм имеет 2 пары параллельных сторон. Это следует из определения параллелограмма - четырехугольника, у которого противоположные стороны попарно параллельны. Если обозначить стороны параллелограмма как AB, BC, CD и DA, то AB параллельна CD, а BC параллельна DA. Это свойство является ключевым при изучении параллелограмма и используется для доказательства других его свойств, например, равенства противоположных сторон и углов, а также того, что диагонали параллелограмма точкой пересечения делятся пополам.

Пояснение:

Утверждение «Все параллельные прямые равны между собой» неверно. Прямые не могут быть равны друг другу, так как они бесконечны и не являются ограниченными отрезками, которые можно сравнить. Параллельные прямые характеризуются тем, что они не пересекаются и находятся на постоянном расстоянии друг от друга, но понятие равенства к ним не применимо. Параллельные прямые могут находиться на разных расстояниях друг от друга, но при этом сохранять свое главное свойство – не пересекаться, даже если продолжить их бесконечно в обе стороны.

Пояснение:

При пересечении двух параллельных прямых третьей прямой (секущей) образуются две пары параллельных отрезков. На рисунке видно, что секущая прямая пересекает параллельные прямые в двух точках, образуя четыре угла: два внутренних и два внешних с каждой стороны. Между этими точками пересечения на параллельных прямых выделяются отрезки, которые можно рассматривать как параллельные. Это построение важно для доказательства признаков параллельности прямых и изучения свойств углов, образованных при пересечении параллельных прямых секущей.

Пояснение:

Четырехугольник с двумя параллельными сторонами называется трапецией. Параллельные стороны трапеции называются основаниями, а две другие, непараллельные стороны - боковыми сторонами. Трапеция является одной из основных геометрических фигур, изучаемых в курсе планиметрии. В зависимости от дополнительных свойств различают виды трапеций: равнобедренную (с равными боковыми сторонами), прямоугольную (с одним прямым углом), произвольную. У трапеции, в отличие от параллелограмма, только одна пара сторон является параллельной.

Пояснение:

Расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из любой точки одной прямой на другую. Это расстояние является постоянной величиной для данной пары параллельных прямых, то есть не зависит от выбора точки. Перпендикуляр - это отрезок, соединяющий точку на одной прямой с другой прямой под углом 90°. Этот перпендикуляр является кратчайшим расстоянием между точкой и прямой, а также между двумя параллельными прямыми. Постоянство расстояния между параллельными прямыми - одно из их ключевых свойств.

Пояснение:

Для построения параллельных прямых используются линейка и угольник (треугольник). Угольник имеет прямой угол, и с его помощью можно точно построить параллельные прямые. Метод заключается в следующем: к данной прямой прикладывают угольник одной из сторон, затем к другой стороне угольника прикладывают линейку. Далее, удерживая линейку неподвижно, сдвигают угольник вдоль линейки до нужной точки и проводят линию вдоль той же стороны угольника. Полученная прямая будет параллельна исходной. Этот метод основан на свойстве параллельности и перпендикулярности.

Пояснение:

Две прямые на плоскости гарантированно не параллельны, если они пересекаются. Это следует непосредственно из определения параллельности: прямые параллельны тогда и только тогда, когда они лежат в одной плоскости и не пересекаются. Если же прямые имеют хотя бы одну общую точку (точку пересечения), то они не могут быть параллельными. Пересекающиеся прямые образуют углы, сумма которых равна 360 градусов. Противоположные углы при этом равны между собой, а смежные в сумме дают 180 градусов.

Пояснение:

Две параллельные прямые по определению никогда не имеют общих точек. Это фундаментальное свойство параллельности: параллельные прямые - это прямые, которые лежат в одной плоскости и не пересекаются, даже если их продолжить бесконечно в обоих направлениях. Если бы прямые имели общую точку, они бы пересекались в этой точке и, следовательно, не были бы параллельными. Понимание этого свойства крайне важно для изучения геометрии и решения задач на параллельность и взаимное расположение прямых в пространстве.

Пояснение:

Для параллельных прямых, пересеченных секущей, верно свойство: накрест лежащие углы равны. Накрест лежащие углы - это углы, которые расположены по разные стороны от секущей и по разные стороны от параллельных прямых. Кроме этого свойства, для параллельных прямых, пересеченных секущей, верны и другие свойства: соответственные углы равны, а сумма односторонних углов равна 180°. Эти свойства используются при решении задач на доказательство параллельности прямых и нахождение неизвестных углов в геометрических конструкциях.

Пояснение:

Прямые, перпендикулярные к одной и той же прямой, параллельны между собой. Это важное следствие из свойств перпендикулярности и параллельности. Данное свойство можно доказать от противного: если предположить, что прямые, перпендикулярные к одной и той же прямой, пересекаются, то через точку их пересечения проходят две различные прямые, перпендикулярные к данной, что противоречит теореме о единственности перпендикуляра к прямой из точки, не лежащей на ней. Это свойство широко применяется в геометрии при решении задач на построение и доказательство.

Пояснение:

В геометрических чертежах часто используются буквы греческого алфавита α и β (альфа и бета) для обозначения параллельных прямых. Это традиция, которая берет свое начало в древнегреческой математике, особенно в работах Евклида. Использование греческих букв помогает отличать обозначения прямых от обозначений точек (для которых обычно используются латинские заглавные буквы) и углов (для которых часто используются другие греческие буквы). Такая система обозначений делает чертежи более информативными и понятными, позволяя легче ссылаться на различные элементы геометрической конструкции.

Пояснение:

С параллельными прямыми связана аксиома Евклида, также известная как пятый постулат Евклида. В современной формулировке она гласит: «Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной». Этот постулат долгое время пытались доказать как теорему, используя остальные аксиомы геометрии, но все попытки оказывались безуспешными. В XIX веке было показано, что пятый постулат независим от остальных аксиом, и на его отрицании были построены неевклидовые геометрии (например, геометрия Лобачевского), где через точку можно провести бесконечно много прямых, параллельных данной.

Пояснение:

Параллельные прямые имеют широкое практическое применение в различных областях деятельности человека. В строительстве они используются при возведении стен, прокладке коммуникаций, установке окон и дверей. В архитектуре параллельность элементов конструкций обеспечивает устойчивость и эстетическую привлекательность зданий. В черчении и инженерном деле параллельные линии используются для создания технических чертежей и схем. В дизайне интерьеров и одежды параллельные линии создают определенный визуальный эффект и стиль. Кроме того, параллельность используется в навигации, картографии, производстве мебели, транспортной инфраструктуре и многих других областях.