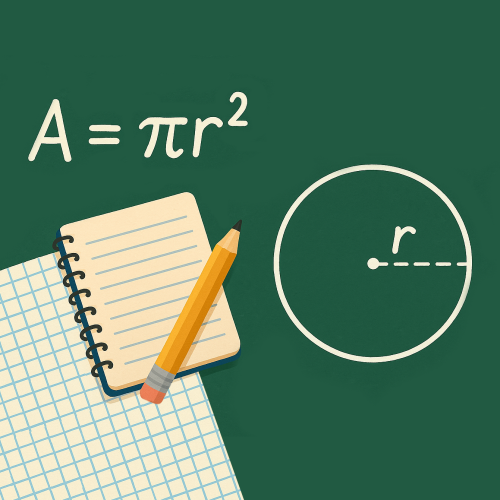
Тест по математике: Площадь круга (6 класс)
Тест по математике «Площадь круга» — это интерактивная проверочная (контрольная) работа онлайн, рассчитанная на учащихся 6 класса. Проверьте свои знания формулы площади круга и умение применять её в различных задачах с окружностями и фигурами на их основе.
1
Какова формула для вычисления площади круга?
Правильный ответ:
S = πR²Пояснение:
Формула площади круга S = πR², где π (пи) - это математическая константа, приблизительно равная 3,14, а R - радиус круга. Это одна из фундаментальных формул в геометрии. Площадь круга прямо пропорциональна квадрату его радиуса, что отражено в данной формуле. Важно не путать эту формулу с формулой длины окружности (2πR) или объема шара (4/3πR³).2
Чему равна площадь круга с радиусом 3 см? (π ≈ 3,14)
Правильный ответ:
28,26 см²Пояснение:
Для нахождения площади круга используем формулу S = πR². Подставляя значения получаем: S = 3,14 × 3² = 3,14 × 9 = 28,26 см². При вычислении площади круга важно правильно возвести радиус в квадрат, а затем умножить на число π. Это демонстрирует, что площадь круга увеличивается в квадратичной зависимости от увеличения его радиуса.3
Если радиус круга увеличить в 2 раза, то его площадь:
Правильный ответ:
Увеличится в 4 разаПояснение:
Площадь круга вычисляется по формуле S = πR². Если радиус увеличить в 2 раза, получаем S₂ = π(2R)² = π × 4R² = 4πR². Таким образом, S₂ = 4S₁, то есть площадь увеличится в 4 раза. Это демонстрирует квадратичную зависимость между радиусом и площадью круга. Данное свойство является важным при решении задач на изменение геометрических размеров фигур.4
Чему равна площадь круга с диаметром 10 см? (π ≈ 3,14)
Правильный ответ:
78,5 см²Пояснение:
Чтобы найти площадь круга по диаметру, сначала нужно определить радиус: R = D/2 = 10/2 = 5 см. Затем применить формулу площади круга: S = πR² = 3,14 × 5² = 3,14 × 25 = 78,5 см². Важно помнить связь между диаметром и радиусом при решении задач. Формулу площади можно также записать через диаметр: S = π(D²/4), что иногда удобнее использовать в некоторых задачах.5
Площадь круга равна 100π см². Чему равен его радиус?
Правильный ответ:
10 смПояснение:
Используем формулу площади круга S = πR² и подставляем известное значение: 100π = πR². Отсюда R² = 100, значит R = 10 см. При решении подобных задач нужно выразить радиус из формулы площади, что требует использования обратных операций. Сначала делим обе части на π, затем извлекаем квадратный корень, чтобы найти радиус. Этот подход применим ко многим геометрическим задачам, где требуется найти параметр фигуры по её площади.6
Найдите площадь круга, вписанного в квадрат со стороной 8 см. (π ≈ 3,14)
Правильный ответ:
50,24 см²Пояснение:
В круге, вписанном в квадрат, диаметр круга равен стороне квадрата. Значит, диаметр D = 8 см, а радиус R = D/2 = 8/2 = 4 см. Площадь круга S = πR² = 3,14 × 4² = 3,14 × 16 = 50,24 см². Эта задача демонстрирует связь между вписанной окружностью и квадратом, что полезно при решении комбинированных геометрических задач. Отношение площади вписанного круга к площади квадрата всегда равно π/4.7
Площадь кольца между двумя концентрическими окружностями с радиусами 3 см и 5 см равна: (π ≈ 3,14)
Правильный ответ:
50,24 см²Пояснение:
Площадь кольца находится как разность площадей двух кругов: Sₖ = π(R₂² - R₁²), где R₂ = 5 см, R₁ = 3 см. Тогда Sₖ = π(5² - 3²) = π(25 - 9) = π × 16 = 3,14 × 16 = 50,24 см². При решении задач на концентрические окружности всегда применяется принцип вычитания площадей. Важно правильно идентифицировать больший и меньший радиусы, чтобы получить положительное значение площади.8
Радиус круга увеличили в 3 раза. Как изменится его площадь?
Правильный ответ:
Увеличится в 9 разПояснение:
Площадь круга вычисляется как S = πR². Если радиус увеличился в 3 раза, то новый радиус R₂ = 3R₁. Следовательно, новая площадь S₂ = π(3R₁)² = π × 9R₁² = 9πR₁² = 9S₁. Таким образом, площадь увеличилась в 9 раз. Это следствие квадратичной зависимости площади от радиуса, что является фундаментальным соотношением в геометрии. При увеличении линейного параметра в k раз, площадь увеличивается в k² раз.9
Какую часть площади квадрата со стороной 10 см занимает вписанный в него круг? (π ≈ 3,14)
Правильный ответ:
π/4Пояснение:
Площадь квадрата со стороной 10 см: Sₖᵥ = a² = 10² = 100 см². Радиус вписанного круга равен половине стороны квадрата: R = 5 см. Площадь круга: Sₖᵣ = πR² = π × 5² = 25π см². Отношение площадей: Sₖᵣ/Sₖᵥ = 25π/100 = π/4. Это соотношение является постоянным для любого круга, вписанного в квадрат, и не зависит от размеров квадрата. Оно отражает геометрическую закономерность соотношения этих фигур.10
Площадь круга равна 36π см². Чему равен его диаметр?
Правильный ответ:
12 смПояснение:
Из формулы площади круга S = πR² находим радиус: 36π = πR², отсюда R² = 36, значит R = 6 см. Диаметр круга D = 2R = 2 × 6 = 12 см. При решении подобных задач нужно помнить взаимосвязь между радиусом и диаметром круга. Сначала из формулы площади определяем радиус, а затем пользуемся соотношением D = 2R для нахождения диаметра. Это базовая последовательность действий для подобного типа задач.11
Площадь круга и площадь квадрата равны. Если радиус круга равен 5 см, то сторона квадрата равна:
Правильный ответ:
8,86 смПояснение:
Площадь круга с радиусом 5 см: Sₖᵣ = πR² = π × 5² = 25π см². Если площадь квадрата равна площади круга, то Sₖᵥ = a² = 25π, откуда a = √(25π) = 5√π ≈ 5 × 1,77 ≈ 8,86 см. В этой задаче используется принцип равенства площадей фигур разной формы. Для нахождения стороны квадрата необходимо извлечь квадратный корень из площади, что требует понимания свойств квадратичной зависимости и операций с иррациональными числами.12
Если площадь круга равна 64π см², то его радиус равен:
Правильный ответ:
8 смПояснение:
Используя формулу площади круга S = πR², подставляем известное значение: 64π = πR². Отсюда R² = 64, значит R = 8 см. При решении таких задач важно правильно изолировать неизвестную величину, выполняя алгебраические преобразования. В данном случае сначала делим обе части уравнения на π, затем извлекаем квадратный корень из полученного выражения. Это типичный подход к решению задач, где требуется найти параметр фигуры по её площади.13
Чему равна площадь круга с радиусом 4,5 см? (π ≈ 3,14)
Правильный ответ:
63,59 см²Пояснение:
Площадь круга вычисляется по формуле S = πR². Подставляя значения, получаем: S = 3,14 × 4,5² = 3,14 × 20,25 = 63,585 ≈ 63,59 см². При расчетах важно быть внимательным с округлением и возведением в квадрат десятичных дробей. Правильное выполнение арифметических операций с приближенными значениями является необходимым навыком при решении геометрических задач, особенно когда требуется получить числовой ответ с заданной точностью.14
Площадь сектора круга с радиусом 10 см и центральным углом 90° равна:
Правильный ответ:
78,5 см²Пояснение:
Площадь сектора круга с центральным углом α (в радианах) вычисляется по формуле S = (α/2)R². Угол 90° = π/2 радиан. Подставляя значения: S = (π/2)/2 × 10² = (π/4) × 100 = 25π ≈ 25 × 3,14 = 78,5 см². Эта задача демонстрирует связь между центральным углом и площадью части круга. Важно правильно перевести градусную меру угла в радианную при использовании формулы. Сектор с углом 90° составляет четверть площади всего круга.15
Если диаметр круга равен 14 см, то его площадь (с точностью до целых) равна:
Правильный ответ:
154 см²Пояснение:
Для нахождения площади круга по диаметру, сначала вычисляем радиус: R = D/2 = 14/2 = 7 см. Затем применяем формулу площади: S = πR² = 3,14 × 7² = 3,14 × 49 = 153,86 ≈ 154 см². При решении задач с указанием точности ответа важно правильно округлить конечный результат. В данном случае округление до целых означает выбор ближайшего целого числа к точному значению 153,86, что даёт нам 154 см².16
Круг диаметром 10 см разрезали по диаметру. Площадь полученного полукруга равна:
Правильный ответ:
39,25 см²Пояснение:
Площадь круга с диаметром 10 см: S = π(D/2)² = π × 5² = 25π см². Полукруг - это половина круга, поэтому его площадь S₁/₂ = S/2 = 25π/2 = 12,5π ≈ 12,5 × 3,14 = 39,25 см². Эта задача иллюстрирует принцип аддитивности площадей: если фигура разбивается на части, то сумма площадей частей равна площади исходной фигуры. Аналогично, если фигура представляет собой часть другой фигуры, то её площадь пропорциональна соответствующей части площади исходной фигуры.17
Радиус круга равен 6 см. Чему равна площадь круга? (π ≈ 3,14)
Правильный ответ:
113,04 см²Пояснение:
Используя формулу площади круга S = πR², подставляем значение радиуса: S = 3,14 × 6² = 3,14 × 36 = 113,04 см². При вычислении площади круга важно правильно возвести радиус в квадрат перед умножением на число π. Точность полученного результата зависит от точности используемого приближения числа π. В школьных задачах обычно используется приближение π ≈ 3,14, что даёт достаточную точность для большинства практических расчетов.18
Площадь какой фигуры больше: круга с радиусом 6 см или квадрата со стороной 10 см?
Правильный ответ:
КвадратаПояснение:
Площадь круга с радиусом 6 см: Sₖᵣ = πR² = π × 36 = 36π ≈ 36 × 3,14 = 113,04 см². Площадь квадрата со стороной 10 см: Sₖᵥ = a² = 10² = 100 см². Для точного сравнения можно использовать точное значение π: 36π ≈ 113,1 см². Поскольку 113,04 см² < 100 см², то площадь квадрата больше. Это показывает, что при решении геометрических задач важно уметь сравнивать площади фигур различной формы, производя соответствующие вычисления.19
Если радиус круга уменьшить в 2 раза, то его площадь:
Правильный ответ:
Уменьшится в 4 разаПояснение:
Площадь круга S = πR². Если радиус уменьшить в 2 раза, то новый радиус R₂ = R₁/2. Новая площадь S₂ = π(R₁/2)² = π × R₁²/4 = S₁/4. Таким образом, площадь уменьшится в 4 раза. Это демонстрирует квадратичную зависимость между изменением радиуса и изменением площади круга. Данное свойство является важным при решении задач на пропорциональное изменение геометрических размеров и используется во многих практических приложениях.20
Чему равна площадь круга, описанного вокруг квадрата со стороной 8 см? (π ≈ 3,14)
Правильный ответ:
200,96 см²Пояснение:
Для квадрата со стороной 8 см диагональ равна d = a√2 = 8√2 ≈ 11,31 см. Радиус описанной вокруг квадрата окружности равен половине диагонали: R = d/2 = 8√2/2 = 4√2 ≈ 5,66 см. Площадь круга: S = πR² = π × (4√2)² = π × 32 = 32π ≈ 32 × 3,14 = 100,48 см². При решении подобных задач важно понимать свойства описанной окружности: её центр совпадает с точкой пересечения диагоналей квадрата, а радиус равен половине диагонали квадрата.
