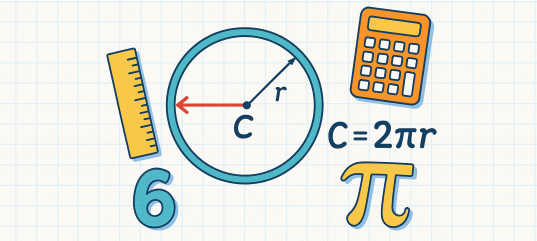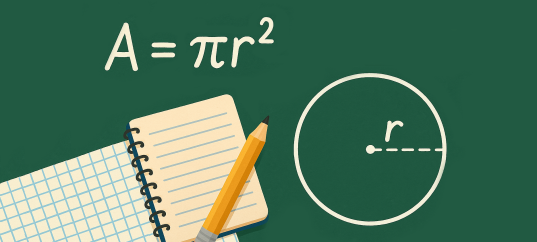Тест по математике: Представления о шаре и сфере (6 класс)

Пояснение:

Сфера — это геометрическая поверхность, образованная множеством всех точек в пространстве, равноудаленных от заданной точки, называемой центром сферы. Это важно отличать от шара, который является телом, ограниченным сферой. Можно провести аналогию: сфера относится к шару так же, как окружность к кругу. Сфера — это именно поверхность, а не сам объем.

Пояснение:

Шар — это геометрическое тело в трехмерном пространстве, которое состоит из всех точек, находящихся на расстоянии, не превышающем заданное (радиус шара), от центральной точки. Другими словами, шар — это объемное тело, ограниченное сферической поверхностью. Это пространственный аналог круга на плоскости. В шар входит как его граница (сфера), так и все внутренние точки.

Пояснение:

Пояснение:

Пояснение:

Пояснение:

Пояснение:

Большой круг сферы — это круг, образованный при пересечении сферы плоскостью, проходящей через центр сферы. Диаметр большого круга совпадает с диаметром сферы. Большие круги делят сферу на две равные части, называемые полусферами. Большие круги имеют важное значение в навигации: например, кратчайший путь между двумя точками на поверхности Земли (если представить её сферой) проходит по дуге большого круга.

Пояснение:

Малый круг сферы — это круг, образующийся при пересечении сферы плоскостью, не проходящей через центр сферы. В отличие от большого круга, малый круг имеет радиус меньше радиуса сферы, и его размер зависит от расстояния от плоскости сечения до центра сферы. Малые круги не делят сферу на равные части. В географии параллели на глобусе, кроме экватора, являются малыми кругами.

Пояснение:

Сечение шара — это фигура, образованная пересечением шара с плоскостью. Сечение шара всегда представляет собой круг. Размер этого круга зависит от расположения секущей плоскости относительно центра шара. Если плоскость проходит через центр шара, то сечением будет большой круг с радиусом, равным радиусу шара. Чем дальше секущая плоскость от центра, тем меньше радиус получаемого круга-сечения.

Пояснение:

Пояснение:

Полюс сферы относительно некоторой плоскости — это точка на перпендикуляре к плоскости, проведенном через центр сферы. Если плоскость пересекает сферу, то получаются два полюса — северный и южный, расположенные на противоположных сторонах от плоскости на равном расстоянии от неё. Полюсы играют важную роль в сферической геометрии и используются, например, в картографии или астрономии для определения ориентации сферы.

Пояснение:

Шар никогда не имеет ребер. Это геометрическое тело с абсолютно гладкой поверхностью без каких-либо углов, граней или ребер. В этом заключается принципиальное отличие шара от многогранников, таких как куб, пирамида или призма, которые имеют грани, ребра и вершины. Поверхность шара — сфера — представляет собой непрерывную гладкую поверхность, где каждая точка находится на одинаковом расстоянии от центра.

Пояснение:

Полусфера — это половина сферы, получаемая при разделении сферы плоскостью, проходящей через её центр. Граница полусферы представляет собой большой круг исходной сферы. Полусферы широко применяются в архитектуре (купола зданий), в навигации (небесная полусфера), в различных технических устройствах и инструментах. Площадь поверхности полусферы равна 2πR², где R — радиус исходной сферы.

Пояснение:

Сфера действительно является поверхностью шара. Это соотношение аналогично соотношению между окружностью и кругом в плоской геометрии. Сфера — это двумерная поверхность в трёхмерном пространстве, состоящая из всех точек, равноудаленных от её центра. Шар же — это трёхмерное тело, включающее в себя как сферическую поверхность, так и все точки внутри этой поверхности. Таким образом, сфера ограничивает шар, являясь его границей.

Пояснение:

Шар не имеет граней. В геометрии грань — это плоская часть поверхности многогранника, ограниченная отрезками прямых (рёбрами). Поверхность шара — сфера — является гладкой криволинейной поверхностью без каких-либо плоских участков. Это одно из ключевых отличий шара от многогранников, таких как куб или тетраэдр, которые имеют плоские грани. Отсутствие граней делает шар уникальным геометрическим телом с особыми свойствами.

Пояснение:

Центр сферы — это точка, которая равноудалена от всех точек поверхности сферы. Расстояние от центра до любой точки на сфере называется радиусом сферы. Это определяющее свойство сферы: все точки её поверхности находятся на одинаковом расстоянии от центра. Центр сферы является ключевой точкой для всех измерений и построений, связанных со сферой. Через центр проходят все диаметры сферы и оси симметрии.

Пояснение:

Пояснение:

Форма Земли в действительности не является идеальной сферой или шаром. Наиболее точной моделью формы Земли является геоид — фигура, близкая к сплюснутому у полюсов эллипсоиду вращения. Из-за вращения вокруг своей оси Земля немного «сплющена» на полюсах и выпячена на экваторе. Экваториальный радиус Земли примерно на 21 км больше полярного. Кроме того, поверхность Земли имеет неровности (горы, впадины), которые также отличают её от идеальной геометрической фигуры.

Пояснение:

Мыльный пузырь имеет форму, наиболее близкую к идеальной сфере из перечисленных объектов. Это объясняется действием сил поверхностного натяжения: мыльная плёнка стремится минимизировать свою площадь при заданном объёме воздуха внутри, а сфера — это фигура с минимальной площадью поверхности при фиксированном объёме. Футбольный мяч состоит из многоугольников, Земля — сплюснутый эллипсоид, а воздушный шарик может иметь различную, не всегда сферическую форму.

Пояснение:

Хорда сферы — это отрезок прямой линии, соединяющий две любые точки, лежащие на поверхности сферы. Хорда, проходящая через центр сферы, называется диаметром и является самой длинной возможной хордой. Длина хорды зависит от её расположения относительно центра сферы: чем ближе хорда к центру, тем она длиннее. Если расстояние от центра сферы до хорды равно d, а радиус сферы равен R, то длина хорды равна 2√(R²-d²).