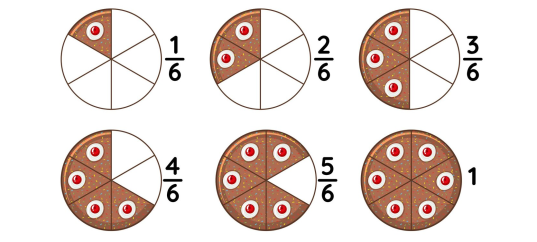
Тест по математике: Обыкновенные дроби — 5 класс
Тест по математике «Обыкновенные дроби» — проверочная (контрольная) работа, рассчитанная на учащихся 5 класса. Вы столкнетесь с задачами на сравнение, сложение, вычитание, умножение и деление дробей, а также на сокращение дробей и нахождение части от числа. Тест поможет вам оценить своё понимание основных концепций работы с обыкновенными дробями и применение этих знаний в задачах.
1
Какая дробь является правильной?
Правильный ответ:
3/5Пояснение:
Правильная дробь — это дробь, у которой числитель меньше знаменателя. В дроби 3/5 числитель 3 меньше знаменателя 5, поэтому она является правильной дробью. Такая дробь всегда меньше единицы. Остальные дроби в ответах — неправильные, так как их числители больше или равны знаменателям, и такие дроби больше или равны единице.2
Какая дробь является неправильной?
Правильный ответ:
9/4Пояснение:
Неправильная дробь — это дробь, у которой числитель больше или равен знаменателю. В дроби 9/4 числитель 9 больше знаменателя 4, поэтому она является неправильной дробью. Такая дробь всегда больше или равна единице. Остальные дроби в ответах — правильные, так как их числители меньше знаменателей, и такие дроби меньше единицы.3
Чему равна сумма дробей 1/4 и 3/4?
Правильный ответ:
1Пояснение:
Чтобы найти сумму дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же. 1/4 + 3/4 = (1+3)/4 = 4/4 = 1. Дробь 4/4 равна единице, так как любое число, делённое на себя, равно 1. Таким образом, сумма дробей 1/4 и 3/4 равна 1. Можно сказать, что эти дроби являются дополнительными до единицы.4
Какая дробь равна 6/8 после сокращения?
Правильный ответ:
3/4Пояснение:
Чтобы сократить дробь 6/8, нужно найти наибольший общий делитель (НОД) числителя и знаменателя, а затем разделить и числитель, и знаменатель на этот НОД. НОД чисел 6 и 8 равен 2. Разделим числитель и знаменатель на 2: 6/8 = (6÷2)/(8÷2) = 3/4. Таким образом, дробь 6/8 после сокращения равна 3/4. Дробь считается несократимой, если НОД числителя и знаменателя равен 1.5
Чему равна разность дробей 7/8 и 1/4?
Правильный ответ:
5/8Пояснение:
Чтобы вычесть дроби, нужно привести их к общему знаменателю. Знаменатель 8 делится на знаменатель 4, поэтому приводим вторую дробь к знаменателю 8: 1/4 = (1×2)/(4×2) = 2/8. Теперь вычитаем: 7/8 - 2/8 = (7-2)/8 = 5/8. Таким образом, разность дробей 7/8 и 1/4 равна 5/8. При вычитании дробей с одинаковыми знаменателями вычитаются только числители.6
Чему равно произведение дробей 2/3 и 3/5?
Правильный ответ:
2/5Пояснение:
Чтобы найти произведение дробей, нужно перемножить их числители и перемножить знаменатели: (2/3) × (3/5) = (2×3)/(3×5) = 6/15. После получения произведения, необходимо проверить, можно ли сократить результат. НОД чисел 6 и 15 равен 3. Поэтому 6/15 = (6÷3)/(15÷3) = 2/5. Таким образом, произведение дробей 2/3 и 3/5 равно 2/5.7
Чему равно частное дробей 3/4 и 2/3?
Правильный ответ:
9/8Пояснение:
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй: (3/4) ÷ (2/3) = (3/4) × (3/2) = (3×3)/(4×2) = 9/8. Таким образом, частное дробей 3/4 и 2/3 равно 9/8 или 1 1/8 (одна целая одна восьмая). Обратите внимание, что при делении дробей мы «переворачиваем» вторую дробь и выполняем умножение.8
Какая дробь равна 3/4 + 1/6?
Правильный ответ:
11/12Пояснение:
Чтобы сложить дроби с разными знаменателями, нужно привести их к общему знаменателю. Наименьший общий знаменатель (НОЗ) чисел 4 и 6 равен 12. Приводим дроби к знаменателю 12: 3/4 = (3×3)/(4×3) = 9/12, 1/6 = (1×2)/(6×2) = 2/12. Теперь складываем: 9/12 + 2/12 = (9+2)/12 = 11/12. Таким образом, сумма дробей 3/4 и 1/6 равна 11/12.9
Чему равна 1/5 от числа 35?
Правильный ответ:
7Пояснение:
Чтобы найти дробь от числа, нужно это число умножить на дробь: 1/5 × 35 = 35 × (1/5) = 35/5 = 7. Можно решить иначе: найти 1/5 от числа — значит разделить это число на 5, то есть 35 ÷ 5 = 7. Таким образом, 1/5 часть от 35 равна 7. Этот принцип применяется при решении задач на нахождение части от числа.10
Сравните дроби 5/9 и 4/7. Какая из них больше?
Правильный ответ:
4/7Пояснение:
Чтобы сравнить дроби с разными знаменателями, приведём их к общему знаменателю. НОЗ чисел 9 и 7 равен 63. 5/9 = (5×7)/(9×7) = 35/63, 4/7 = (4×9)/(7×9) = 36/63. Теперь можно сравнить числители: 35 < 36, значит 35/63 < 36/63, а следовательно, 5/9 < 4/7. Другой метод: можно сравнить перекрёстно: 5×7 = 35, 4×9 = 36. Поскольку 35 < 36, то 5/9 < 4/7.11
Какая дробь соответствует 75%?
Правильный ответ:
3/4Пояснение:
Чтобы перевести проценты в дробь, нужно разделить процент на 100: 75% = 75/100. Затем сократить дробь, если возможно. НОД чисел 75 и 100 равен 25. Поэтому 75/100 = (75÷25)/(100÷25) = 3/4. Таким образом, 75% соответствует дроби 3/4. В общем виде, чтобы перевести процент в дробь, нужно записать его как отношение к 100 и сократить, если возможно.12
Какая из следующих дробей наименьшая?
Правильный ответ:
2/5Пояснение:
Чтобы сравнить дроби с разными знаменателями, приведём их к общему знаменателю или используем перекрёстное умножение. Применим второй способ. Для 2/5 и 3/7: 2×7 = 14, 3×5 = 15. Так как 14 < 15, то 2/5 < 3/7. Для 2/5 и 4/9: 2×9 = 18, 4×5 = 20. Так как 18 < 20, то 2/5 < 4/9. Для 2/5 и 5/11: 2×11 = 22, 5×5 = 25. Так как 22 < 25, то 2/5 < 5/11. Таким образом, наименьшая дробь — 2/5.13
Чему равно 2/3 + 5/6 - 1/4?
Правильный ответ:
5/4Пояснение:
Приведём дроби к общему знаменателю. НОЗ чисел 3, 6 и 4 равен 12. 2/3 = (2×4)/(3×4) = 8/12, 5/6 = (5×2)/(6×2) = 10/12, 1/4 = (1×3)/(4×3) = 3/12. Выполним вычисления: 8/12 + 10/12 - 3/12 = (8+10-3)/12 = 15/12. Дробь 15/12 можно представить как смешанное число: 15/12 = 1 3/12 = 1 1/4, или сократить: 15/12 = (15÷3)/(12÷3) = 5/4.
14
Какую часть часа составляют 40 минут?
Правильный ответ:
2/3Пояснение:
В одном часе 60 минут. Чтобы найти, какую часть часа составляют 40 минут, нужно составить дробь: 40/60. Затем сократить её, если возможно. НОД чисел 40 и 60 равен 20. Поэтому 40/60 = (40÷20)/(60÷20) = 2/3. Таким образом, 40 минут составляют 2/3 часа. Другими словами, 40 минут — это две трети часа.15
Чему равно произведение дробей 1/2, 2/3 и 3/4?
Правильный ответ:
1/4Пояснение:
Чтобы найти произведение нескольких дробей, нужно перемножить все числители и перемножить все знаменатели: (1/2) × (2/3) × (3/4) = (1×2×3)/(2×3×4) = 6/24. После получения произведения, необходимо проверить, можно ли сократить результат. НОД чисел 6 и 24 равен 6. Поэтому 6/24 = (6÷6)/(24÷6) = 1/4. Таким образом, произведение дробей 1/2, 2/3 и 3/4 равно 1/4.16
Найдите значение выражения: (2/5) ÷ (3/10)
Правильный ответ:
4/3Пояснение:
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй: (2/5) ÷ (3/10) = (2/5) × (10/3) = (2×10)/(5×3) = 20/15. После получения результата, необходимо проверить, можно ли сократить дробь. НОД чисел 20 и 15 равен 5. Поэтому 20/15 = (20÷5)/(15÷5) = 4/3. Таким образом, значение выражения (2/5) ÷ (3/10) равно 4/3 или 1 1/3.17
Автомобиль израсходовал 3/8 бака бензина. Какая часть бака осталась заполненной?
Правильный ответ:
5/8Пояснение:
Если изначально бак был полным (что подразумевается в задаче), то его объём составлял 1 (или 8/8 в виде дроби с знаменателем 8). Если израсходована 3/8 часть бака, то оставшаяся часть составляет 1 - 3/8 = 8/8 - 3/8 = (8-3)/8 = 5/8. Таким образом, в баке осталось 5/8 от его полного объёма. Это типичный пример задачи на нахождение дополнительной части до целого.18
Запишите смешанное число 2 3/5 в виде неправильной дроби
Правильный ответ:
13/5Пояснение:
Чтобы перевести смешанное число в неправильную дробь, нужно умножить целую часть на знаменатель дробной части, прибавить к результату числитель дробной части и записать полученную сумму как числитель новой дроби. Знаменатель остаётся прежним. Для числа 2 3/5: 2×5 + 3 = 10 + 3 = 13. Таким образом, 2 3/5 = 13/5. Такое преобразование часто используется при операциях с дробями.19
Какое смешанное число соответствует неправильной дроби 17/4?
Правильный ответ:
4 1/4Пояснение:
Чтобы перевести неправильную дробь в смешанное число, нужно разделить числитель на знаменатель. Целую часть составляет неполное частное, а дробную — остаток от деления, записанный в виде дроби с тем же знаменателем. Для дроби 17/4: 17 ÷ 4 = 4 (целая часть) и остаток 1. Значит, 17/4 = 4 1/4. Проверка: 4 1/4 = (4×4 + 1)/4 = (16 + 1)/4 = 17/4.20
Сколько минут составляют 3/4 часа?
Правильный ответ:
45 минутПояснение:
В одном часе 60 минут. Чтобы найти, сколько минут составляют 3/4 часа, нужно 60 минут умножить на 3/4: 60 × (3/4) = (60×3)/4 = 180/4 = 45 минут. Таким образом, 3/4 часа составляют 45 минут. Этот принцип можно применять при переводе частей часа в минуты: 1/4 часа = 15 минут, 1/2 часа = 30 минут, 3/4 часа = 45 минут.
